13 💻 Intermediate prep
I addressed the issue with Professor G. Arbia, and we agreed that the intermediate test topics should include: - hypothesis tests on means - anova - simple + multiple regression
We rule out logistic regression 👍
Below you find a bunch of exercises which in some way may resemble intermediate ones.
13.1 🪨 core concepts of T test
recall from Arbia’s slide 69 that we are focusing on test on mean and that steps for calculating statistical tests generally are:
- Develop the null Hypothesis
- Specify the level of Significance
- Collect the sample data and compute the test statistic.
then pvalues: 4. Use the value of the test statistic to compute the p-value 5. Reject if p-value $ < $
Notice that Z-test are not really used since we almost always do not know the variance of the distribution. So instead of Standard Normal distribution we use Student’s T distribution, doing t-tests. That’s the t test stat:
Below all the possible cases you should be dealing with:
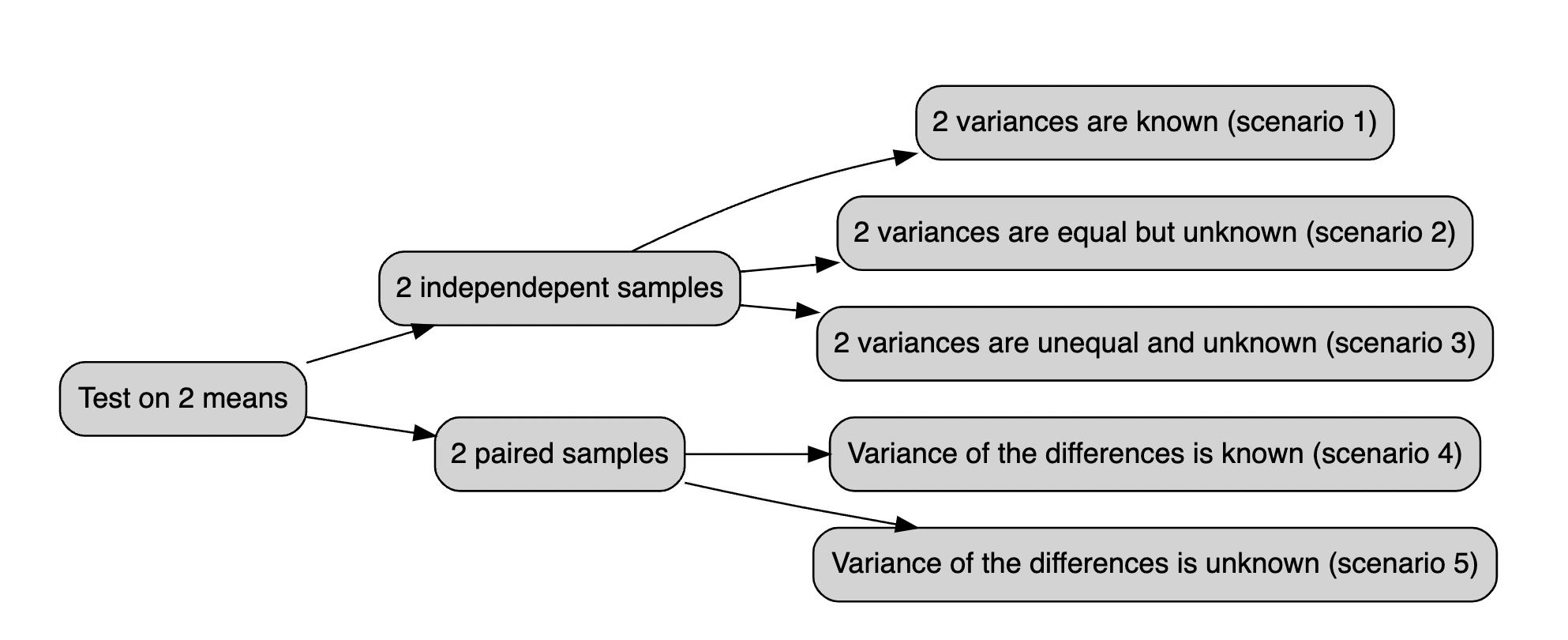
wf
13.2 t.test() function
The t.test() function may run one and two sample t-tests on data vectors. The function has several parameters and is invoked as follows:
t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0,
paired = FALSE, var.equal = FALSE, conf.level = 0.95)In this case, x is a numeric vector of data values, and y is optional. If y is not included, the function does a one-sample t-test on the data in x; if it is included, the function runs a two-sample t-test on both x and y.
The mu (i.e. ) argument returns a number showing the real value of the mean (or difference in means if a two sample test is used) under the null hypothesis. The test conducts a two-sided t-test by default; however, you may perform an alternative hypothesis by changing the alternative argument to "greater" or "less", depending on whether the alternative hypothesis is that the mean is larger than or smaller than mu. Consider the following:
t.test(x, alternative = "less", mu = 25)…performs a one-sample t-test on the data contained in x where the null hypothesis is that $ = 25$ and the alternative is that $ < 25 $
The paired argument will indicate whether or not you want a paired t-test. The default is set to FALSE but can be set to TRUE if you desire to perform a paired t-test. We do paired test when we are considering pre-post treatment test or when we are considering couples of individuals.
When doing a two-sample t-test, the var.equal option specifies whether or not to assume equal variances. The default assumption is unequal variance and the Welsh approximation to degrees of freedom; however, you may change this to TRUE to pool the variance.
Finally, the conf.level parameter specifies the degree of confidence in the reported confidence interval for in the one-sample and for two-sample cases. Below a very simple example:
13.3 class exercises, do it groups 👯
first guided,
Exercise 13.1 A state Highway Patrol periodically samples vehicle at various location on a particular roadway. The sample of vehicle speed is used to test the hypothesis H0 for which the mean is less than equal to 65
The locations where is rejected are deemed the best locations for radar traps. At location F, a sample of 64 vehicles shows a mean speed of 66.2 mph with a std dev of 4.2 mph. Use a to test the hypothesis.
Answer to Exercise 13.1:
Sample random data from a Normal distribution with a given mean and sd. Then define H0 and H1. In the end run hte test.
x <- rnorm(n = 64, mean = 66.2, sd = 4.2)
test<-t.test(x, mu = 65, alternative = "less")
t = 1.469, df = 63, p-value = 0.9266
alternative hypothesis: true mean is less than 65
95 percent confidence interval:
-Inf 66.80805
sample estimates:
mean of x
65.84629 The One Sample t-test testing the difference between x (mean = 65.85) and mu = 65 suggests that the effect is positive, statistically not significant, and very small (difference = 0.85, 95% CI [-Inf, 66.81], t(63) = 1.47, p = 0.927
Exercise 13.2 Let’s assume to have dataset midwest in ggplot2 package: this contains demographic information of midwest counties from 2000 US census.
Besides all the other variables we are interested in percollege which describes the Percent college educated in midwest.
- test if the midwest average is less than the national average (i.e. *35%) with a p-value < .02.
Exercise 13.3 Download the datafile ‘prawnGR.CSV’ from the Data link and save it to the data directory (Remember R projects and working directory). Import these data into R and assign to a variable with an appropriate name. These data were collected from an experiment to investigate the difference in growth rate of the giant tiger prawn (Penaeus monodon) fed either an artificial or natural diet.
- Have a quick look at the structure of this dataset.
- plot the growth rate versus the diet using an appropriate plot.
- How many observations are there in each diet treatment?
- You want to compare the difference in growth rate between the two diets using a two sample t-test.
- Conduct a two sample t-test using the t.test() using the argument
var.equal = TRUEto perform the t-test assuming equal variances. What is the null hypothesis you want to test? Do you reject or fail to reject the null hypothesis? What is the value of the t statistic, degrees of freedom and p value? How would you summarise these summary statistics in a report?
Exercise 13.4 A new coach has been hired at an athletics school, and the effectiveness of the new type of training will be evaluated by comparing the average times of 10 centimeters. The times in seconds before and after each athlete’s competition are repeated.ù
before_training: = c(12.9, 13.5, 12.8, 15.6, 17.2, 19.2, 12.6, 15.3, 14.4, 11.3)
after_training = c( 12.7, 13.6, 12.0, 15.2, 16.8, 20.0, 12.0, 15.9, 16.0, 11.1)We are up against two groups of trained competitors, as measurements were taken on the same athletes before and after the competition. To determine if there has been an improvement, a deterioration, or if the time averages have remained essentially constant (i.e., H0). Conduct a test t of student for paired changes if the difference significant to a 95% confidence level?
Exercise 13.5 Following exercise 4 Assume that the club management, based on the statistics, fires this coach who has not improved and hires another more promising coach. Following the second training session, we record the athletes’ times:
before training: 12.9, 13.5, 12.8, 15.6, 17.2, 19.2, 12.6, 15.3, 14.4, 11.3
after training: 12.0, 12.2, 11.2, 13.0, 15.0, 15.8, 12.2, 13.4, 12.9, 11.0Exercise 13.6 Let’s assume genderweight in datarium package, containing the weight of 40 individuals (20 women and 20 men).
- which are the mean weights for male and females?
- test is they are statistically significant with 95% confidence level
13.4 ☄️ ANOVA
ANOVA (ANalysis Of VAriance) is a statistical test to determine whether two or more population means are different. In other words, it is used to compare two or more groups to see if they are significantly different.
In practice, however, the:
- Student t-test is used to compare 2 groups;
- ANOVA generalizes the t-test beyond 2 groups, so it is used to compare 3 or more groups.
Although ANOVA is used to make inference about means of different groups, the method is called “analysis of variance.” It is called like this because it compares the “between” variance (the variance between the different groups) and the variance “within” (the variance within each group). If the between variance is significantly larger than the within variance, the group means are declared to be different. Otherwise, we cannot conclude one way or the other. The two variances are compared to each other by taking the ratio :
Below are the assumptions of the ANOVA, how to test them and which other tests exist if an assumption is not met:
- variable type: ANOVA requires a mix of one continuous quantitative dependent variable (which corresponds to the measurements to which the question relates) and one qualitative independent variable (with at least 2 levels which will determine the groups to compare).
- Independence: the data, collected from a representative and randomly selected portion of the total population, should be independent between groups and within each group.
- Normality
- Equality of variances: the variances of the different groups should be equal in the populations (an assumption called homogeneity of the variances, or even sometimes referred as homoscedasticity, as opposed to heteroscedasticity if variances are different across groups)
- Outliers: there should not be significant outliers in different groups.
There are a bunch of cases you should be dealing with, here they are:
- Check that your observations are independent.
- Sample sizes:
- In case of small samples, test the normality of residuals:
- If normality is assumed, test the homogeneity of the variances:
- If variances are equal, use ANOVA.
- If variances are not equal, use the Welch ANOVA.
- If normality is not assumed, use the Kruskal-Wallis test.
- If normality is assumed, test the homogeneity of the variances:
- In case of small samples, test the normality of residuals:
- In case of large samples normality is assumed, so test the homogeneity of the variances:
- If variances are equal, use ANOVA.
- If variances are not equal, use the Welch ANOVA.
13.5 aov() function
Data for this exercise is the penguins dataset (an alternative to the well-known iris dataset), accessible via the palmerpenguins package:
# install.packages("palmerpenguins")
library(palmerpenguins)
pinguini = penguins[,c("species", "flipper_length_mm")]The dataset contains data for 344 penguins of 3 different species (Adelie, Chinstrap and Gentoo). The dataset contains 8 variables, but we focus only on the flipper length i.e. flipper_length_mm and the species i.e. species, so we keep only those 2 variables.
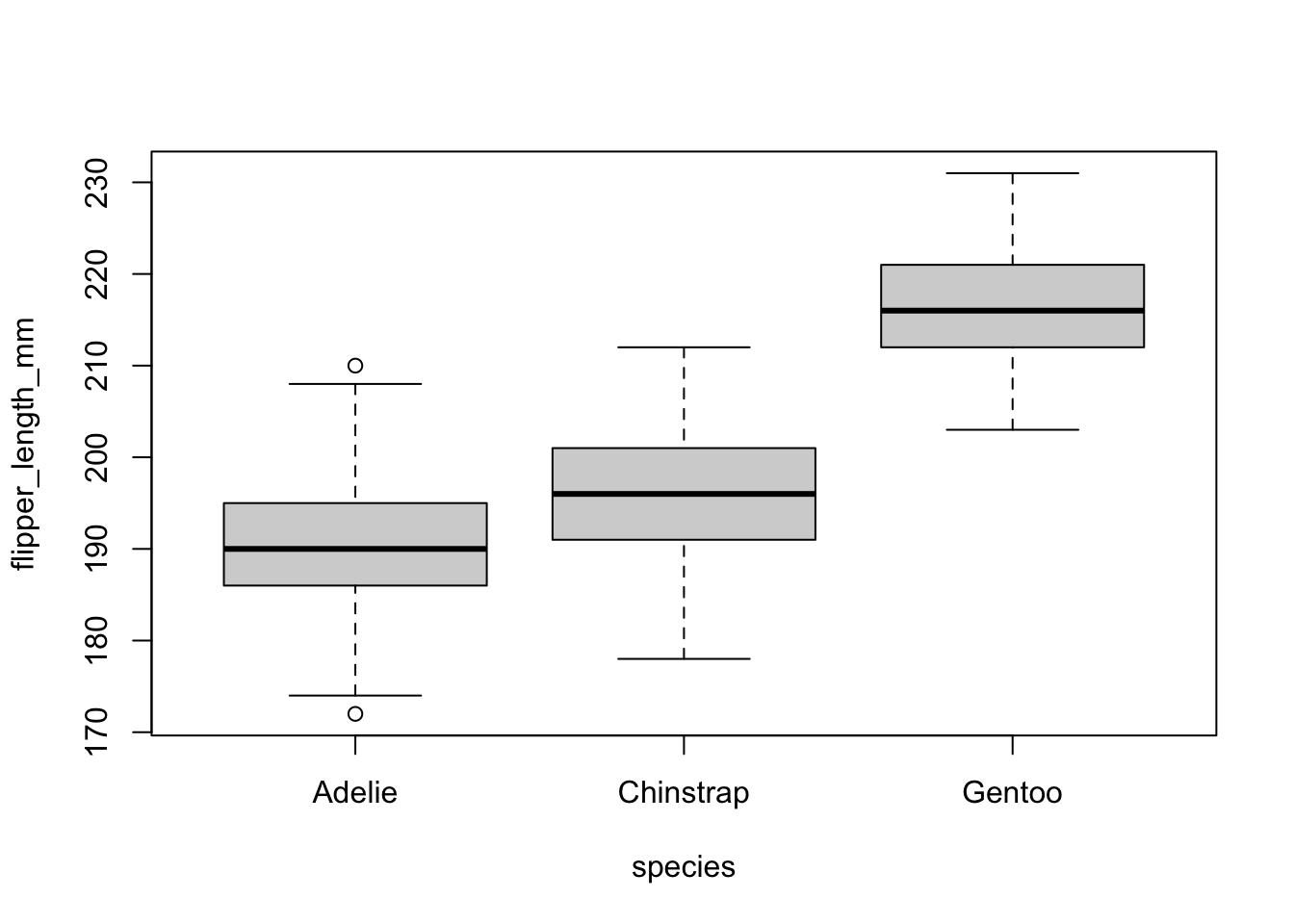
We may want to give a quick check to the groups for a visual inspection:
boxplot(flipper_length_mm ~ species,
data = pinguini
)
then aov(). the fuction take 2 arguments:
-
formula: left side the numeric variable, right side groups i.e.var ~ groups(much like linear regression) -
data: your data
Please refer to (tips) to undestand why data needs to come to longer format to be able to use that.
anova_pinguini =aov(flipper_length_mm ~ species,
data = pinguini
)
anova_pinguini
#> Call:
#> aov(formula = flipper_length_mm ~ species, data = pinguini)
#>
#> Terms:
#> species Residuals
#> Sum of Squares 52473.28 14953.26
#> Deg. of Freedom 2 339
#>
#> Residual standard error: 6.641529
#> Estimated effects may be unbalanced
#> 2 observations deleted due to missingness13.6 class exercises, do it groups 👯
fist guided.
Exercise 13.7 Let’s assume to have a sample with this data and respective belonging group:
x<-c(12,23,12,13,14,21,23,24,30,21,12,13,14,15,16)
z<-c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)perform anova test with aov() function testing if there is significant differences between group 1, 2 and 3.
You specify the formula, where x is the continous variable and y is the group variable.
This is how you solve it.
Answer to Exercise 13.7:
x <- c(12,23,12,13,14,21,23,24,30,21,12,13,14,15,16)
z <- c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)
anova <- aov( x ~ z )
summary(anova)
Df Sum Sq Mean Sq F value Pr(>F)
z 1 1.6 1.60 0.047 **0.832**
Residuals 13 446.1 34.32The ANOVA (formula: x ~ z) suggests that the main effect of z is statistically not significant and very small (F(1, 13) = 0.05, p = 0.832; Eta2 = 3.57e-03, 95% CI [0.00, 1.00]). That means that group means are not that different one from the other
Exercise 13.8 Let’s consider the diet dataset in this link here The data set contains information on 76 people who undertook one of three diets (referred to as diet A, B and C). There is background information such as age, gender, and height. The aim of the study was to see which diet was best for losing weight.
to read data first dowload it from the link, then move data inside your R project. then run these commands:
diet = read.csv("< the dataset name>.csv")We will be using variable Diet, pre.weight and weight6weeks
- read data from kaggle
- compute mean weights for each group
- calculate anova on Diet against the weight cut
Exercise 13.9 We recruit 90 people to participate in an experiment in which we randomly assign 30 people to follow either program A, program B, or program C for one month.
#make this example reproducible
set.seed(0)
#create data frame
data <- data.frame(program = rep(c("A", "B", "C"), each = 30),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
- plot boxplot of weight_loss ~ program Hint: use
boxplot()function specifying the formula. - fit 1 way anova to test difference in weight loss for each program.
Exercise 13.10 Consider the maximum size of 4 fish each from 3 populations (n=12). We want to use a model that will help us examine the question of whether the mean maximum fish size differs among populations.
size <- c(3,4,5,6,4,5,6,7,7,8,9,10)
pop <- c("A","A","A","A","B","B","B","B","C","C","C","C")- visualize it through boxplot
- Using ANOVA model test whether any group means differ from another.
Exercise 13.10 Let’s consider 6 different insect sprays in InsectSprays contained in R. Let’s assume we are interested in testing if there was a difference in the number of insects found in the field after each spraying, use varibales count and spray.
13.7 🍬 tips and tricks
Yout might be interested in standardizing/fornalize how you say things with a statistical jargon, report does that for you.
you simply pass the test, wether it is ANOVA or t.test object inside report report(). Do you rememer the function summary() we have been using for linear regression? This is exactly that, but for both ANOVA and t tests.
# install.packages("remotes")
# remotes::install_github("easystats/report")
library(report)
x <- rnorm(n = 64, mean = 66.2, sd = 4.2)
test<-t.test(x, mu = 65, alternative = "less")
report(test)
#> Effect sizes were labelled following Cohen's (1988)
#> recommendations.
#>
#> The One Sample t-test testing the difference between x
#> (mean = 66.62) and mu = 65 suggests that the effect is
#> positive, statistically not significant, and small
#> (difference = 1.62, 95% CI [-Inf, 67.57], t(63) = 2.84, p =
#> 0.997; Cohen's d = 0.36, 95% CI [-Inf, 0.57])when you have data in longer fromat there a different in syntax when you specify t test and it pretty much follows the one for linear models i.e. lm().
let’s look at it.
we may have something like:
library(tibble)
longer = tribble(
~group, ~var,
"a", 10,
"b", 24,
"a", 31,
"a", 75,
"b", 26,
"a", 8,
"b", 98,
"b", 62,
)
wider = tribble(
~group_a, ~group_b,
10, 24,
31, 26,
75, 98,
8, 62
)Those are exaclty the same dataset but arranged in a different format. We are used to the wider format but iut might happen that we bump into the longer one. What do we do? There’sa trick for that, let’s say you want to test if the mean are statistically different with a 95% confidence level, the instead of supplying x and y to t.test() you would follow pretty much the syntax for linear models lm():
test_for_wider_format = t.test(var~group, data = longer)
test_for_wider_format
#>
#> Welch Two Sample t-test
#>
#> data: var by group
#> t = -0.91809, df = 5.9192, p-value = 0.3944
#> alternative hypothesis: true difference in means between group a and group b is not equal to 0
#> 95 percent confidence interval:
#> -78.99271 35.99271
#> sample estimates:
#> mean in group a mean in group b
#> 31.0 52.5what we conclude? we conclude that: Effect sizes were labelled following Cohen’s (1988) recommendations.
The Welch Two Sample t-test testing the difference of var by group (mean in group a = 31.00, mean in group b = 52.50) suggests that the effect is negative, statistically not significant, and medium (difference = -21.50, 95% CI [-78.99, 35.99], t(5.92) = -0.92, p = 0.394; Cohen’s d = -0.75, 95% CI [-2.39, 0.94])