11 💻 Intermediate results!

Generally you did really and surprisingly well in coding part. This is not true for theory which you should stress more.

11.0.1 👨‍🎓 2022/2023 intermediate (4-11-2022)

Exercise 11.1 Using the dataset Boston downloaded from the library spdep, calculate the coefficient of skewness of the variable RM.

Some of view has faced it, you did not do int during lecture, we took care of that and we assigned max score even if you did it wrong.

Answer to Question 11.1:

library(spdep)

you are not required to load data in this case since the package already does it for you. SO you just need to type boston.c and you find it. Then you need to extract RM

RM_var = boston.c$RM

There are a nunber of packages that makes you able to compute skewness, there are some: e1071, moments, PerformanceAnalytics etc. I will suggest to use moments. So if you dont have it installed execute:

install.packages("moments")
library(moments)

Then use teh function skewnes on RM_var

skewness(RM_var)

Exercise 11.2 How do you define the significance of a statistical test?

Answer to Question 11.2:

The probability of type I error, The probability of rejecting H0 when H0 it is true

Exercise 11.3 What is the power of statistical test?

Answer to Question 11.3:

1 minus the probability of type II error, The probability of accepting H0 when H0 it is true.

Exercise 11.4 How do you define the confidence of a statistical test?

Answer to Question 11.4:

The probability of accepting H0 when H0 it is true.

Exercise 11.5 A law company is evaluating the performances of two departments measuring in terms of the time required for solving a conflict in the last year. The observed values are reported in the following table:

perf_table = data.frame(
  stringsAsFactors = FALSE,
             month = c("january","febraury","march",
                       "april","may","june","july","august","september",
                       "october","november","december"),
            dept_1 = c(NA, NA, NA, 3L, 6L, 9L, 7L, 5L, 7L, 3L, 4L, 6L),
            dept_2 = c(4L, 3L, 9L, 5L, 7L, 2L, 6L, 3L, 6L, 7L, 4L, 1L)
)
)

can we reject the hypothesis H0: (the mean of Dept 1 is equal to the mean of Dept 2) versus a bilateral alternative hypothesis?

This is a t test comparing means for two different samples i.e. depts (dept_1, dept_2), two.sided, not paired (are we talking about the same individuals? is it something like pre and post treatment?)

Answer to Question 11.5:

H0: $μ_{d e p t 1} = μ_{d e p t 2}$ H1: $μ_{d e p t 1} \neq μ_{d e p t 2}$

Remember you always test the alternative hypothesis H1. If the pvalue for the t test is not statistically significant then you reject H1 and conversely you accept H0, in this case means being the same (they are different but that’s because of randomness in data, i.e. sampling variation).

t.test(x = perf_table$dept_1, y = perf_table$dept_2, paired = F, alternative = "two.sided")

Then we look at the p-value for this test and we see something like: 0.4076, so we can conclude that the Two Sample t-test testing the difference between dept_1 and dept_2 (mean of dept_1 = 5.56, mean of dept_2 = 4.75) suggests that the effect is positive, statistically not significant, and small. So we reject the alt. hypo H1 and accept H0.

The question tells you if you can reject the Null Hypo, this is not the case since you just accepted it!

Exercise 11.6 A company has recorded the number of costumers in 10 sample stores before (variable X) and after (Variable Y) a new advertising campaign was introduced. The observed values are reported in the following table:

stores = data.frame(
     n_store = c(1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L),
      before = c(113L, 110L, 108L, 108L, 103L, 101L, 96L, 101L, 104L, 98L),
       after = c(125L, 113L, 115L, 117L, 105L, 112L, 100L, 103L, 116L, 104L)
)

can we reject the hypothesis H0: (the mean of X, i.e. before is equal to the mean of Y, i.e. after) versus a bilateral alternative hypothesis?

Answer to Question 11.6:

This is exactly the same reasoning as before except that this is a paired t test. “Are we talking about the same individuals? are we checking individuals pre and after a treatment?” YES

t.test(x = stores$before, y = stores$after, paired = T, alternative = "two.sided")

Look at the p-value: p-value = 0.0004646.this is really small. SO we can conclude that the Paired t-test testing the difference between before and after (mean difference = -6.80) suggests that the effect is negative, statistically significant, and large.

Exercise 11.7 Write the line of the R command that you use to simulate 2000 random observation from normal distribution with 0 mean and variance = 0.1

Many of you fall into this trap!. Tip: always use the “tab” for automatic suggestion but also check what are arguments. In this case exercise wants you to sample from a normal distribution with 2000 instances (data points), 0 mean and variance = 0.1. The argument in rnorm is sd not var, so you have to apply the square root!

Answer to Question 11.7:

rnorm(n = 2000, mean = 0, sd = 0.1^(1/2))

Exercise 11.8 Write the line of the R command that you use to produce a boxplot of the variable X

This was not mistaken. Assuming you don’t have X, you just need to provide the command to execute boxplot, not actually running it.

Answer to Question 11.8:

boxplot(X)

Exercise 11.9 Given the following 2 variables X = (5,5,3,3,5,5) and Y= (4,4,3,3,3,3), test if the mean of X is significantly different from the mean of Y. Report the p-value of the appropriate test and your decision.

Pretty simple this too.

Answer to Question 11.9:

you at first define vectors X and Y by executing:

X = c(5,5,3,3,5,5)
Y = c(4,4,3,3,3,3)
t.test(X, Y, alternative = "two.sided", paired = F)

so the answer may look something like: The (Welch, remember we did not check variance so we rely on default R behavior applying a transformation to t.test) Sample t-test testing the difference between X and Y (mean of x = 4.33, mean of y = 3.33) suggests that the effect is positive, statistically not significant, and large given the pvalue being 0.0697. However this would also be significant if the alpha level of significance was 10%.

Exercise 11.10 Using the dataset boston.c downloaded from the library spdep, write the elements of the correlation matrix of the variables MEDV, NOX and CRIM.

When you are interested in correlation matrices you are interested in how one variable impact the behavior of the others. Remember we should avoid this in linear regression since it causes a problem called multicollinearity, you should avoid that, a way to check multicollinearity ex-post could be inspecting correlation matrix, a further way ex-post can be by executing VIF on model. You are not interested also in every variable of boston.c, but just MEDV, NOX and CRIM, so you select them (e.g. use select()). Then run correlation with cor()

Answer to Question 11.10:

library(spdep)
library(dplyr)
new_boston = select(boston.c, MEDV, NOX, CRIM)
cor(new_boston)

Note that the principal diag for the matrix is all 1s. This is because you a variables has perfect correlation with itself. You are just interested in the upper triangle. You might also be interested in visualizing it with corrplot. Install it install.packages("corrplot") then pass the matrix as the argument corrplot(cor(new_boston))

Exercise 11.11 Without using formulae, describe how you can calculate the test statistics in a hypothesis testing procedure on a single mean with known variance.

Answer to Question 11.11:

the test statistic is calculated seeing, for example, how many times the absolute difference between the sample mean and the population mean (sm-mu) embodies the standard error = sqrt[(known variance)/n]. This value allow us to standardize the distribution and allocate the value in a Normal distribution (if the variance is known) or in a T di Student distribution (variance unknown) - looking at this value we can now calculate the probability that it is within the range of values established by the level of confidence of the statistical test.

Exercise 11.12 The HR office of a cleaning company wants to test if there is significant difference in the salary between males and females. Call X = the salary of a set of 2000 male workers and Y = the salary of a set of 150 female workers. From previous survey we know that the variances of the two groups are equal. Write the line R command to run an appropriate test of hypothesis.

Here we assume we have data even if we don’t.

Answer to Question 11.12:

t.test(X, Y, paired = F, alternative ="less", var.equal = T)

Exercise 11.13 We want to test statistically the hypothesis that the students at UCSC in Rome have better performances in the second year than in first year year. Can we say that this is a paired sample test?

This need some clarification as one of you colleagues suggested. We are not talking about y’all in two different years bu exact same class, indeed actually and utterly different individuals i.e. your colleague from previous year and y’all.

Answer to Question 11.13:

FALSE

Exercise 11.14 Using the dataset iris test if there is a significant difference between the mean of Petal.Length and the mean of Sepal.Width and report the outcome value of the t-test.

iris comes default in R, you should not load it, this happens also for mtcars

Answer to Question 11.14:

t.test(x = iris$Petal.Length, y = iris$Sepal.Width, alternative = "two.sided", paired = FALSE)

which results is a t-value of 4.3093 and also concluding that (Welch) Two Sample t-test testing the difference between Petal.Length and Sepal.Width (mean of x = 3.76, mean of y = 3.06) suggests that the effect is positive, statistically significant, and medium

Exercise 11.15 Using the dataset iris calculate the correlation between Sepal.Length and Sepal.Width.

simple correlation aight?!

Answer to Question 11.15:

cor(x = iris$Sepal.Length, y = iris$Sepal.Width)

Exercise 11.16 Using the dataset iris report the highest correlation coefficient that you find between the four variables.

Please note that correlation with cor() can be computed with only numeric values. Looking at iris you see the variable species which is a factor (aka grouping variable) we used that for ANOVA aov() when we are interested in comparing means across more than 2 groups. As a result you need to select all the variables but Species and do cor().

Answer to Question 11.16:

iris_filtr = select(iris, Sepal.Length, Sepal.Width, Petal.Length, Petal.Width)
cor(iris_filtr)

there’s another way to do the filtering stuff, you just deselect Species such that:

iris_filtr2 = select(iris, -Species)
cor(iris_filtr2)

You also might want to visualize the correlation as we did before:

library(corrplot)
#> corrplot 0.92 loaded
iris_filtr2 = select(iris, -Species)
corrplot::corrplot(cor(iris_filtr2))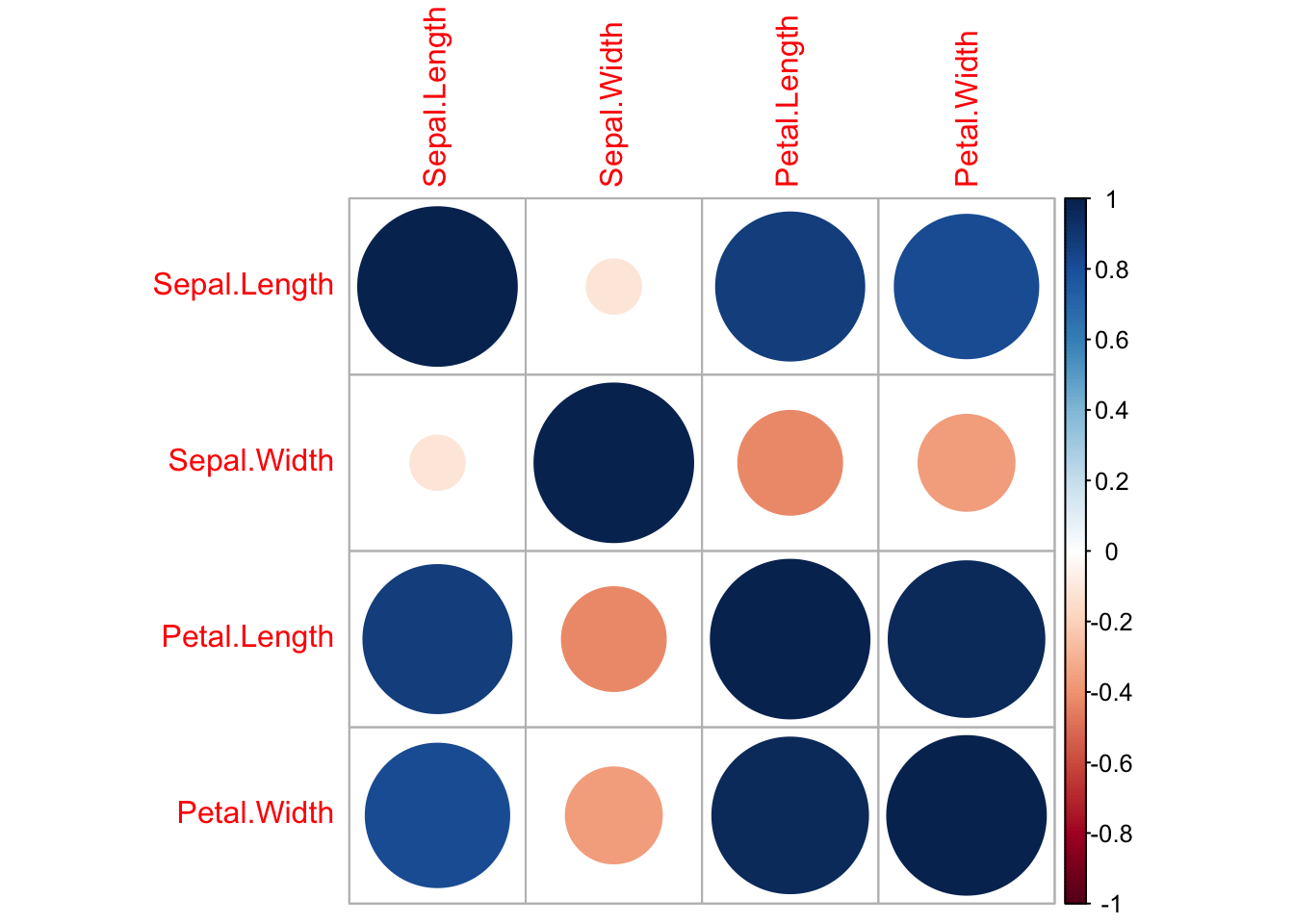

Exercise 11.17 Using the dataset iris report the highest correlation coefficient that you find between the four variables.

Answer to Question 11.17:

iris_filtr = select(iris, Sepal.Length, Sepal.Width, Petal.Length, Petal.Width)
cor(iris_filtr)

there’s another way to do the filtering stuff, you just deselect Species such that:

iris_filtr2 = select(iris, -Species)
cor(iris_filtr2)

Exercise 11.18 Using the dataset iris report the variance of Sepal.Length

Answer to Question 11.18:

var(iris$Sepal.Length)

Exercise 11.19 Using the dataset iris report the third quartile of Sepal.Length

This was not explained during class and it was offered as a bonus question. If you were brave a good enough to have tried it then this have got you a 1 point more.

Answer to Question 11.19:

summary(iris$Sepal.Length)

Exercise 11.20 What is the reason for adjusting the R2 in a multiple regression?

Many of you fall into it. Adjusted R2 is a corrected goodness-of-fit (model accuracy) measure for linear models. It identifies the percentage of variance in the target field that is explained by the input or inputs. R2 tends to optimistically estimate the fit of the linear regression. It always increases as the number of effects are included in the model. Adjusted R2 attempts to correct for this overestimation. Adjusted R2 might decrease if a specific effect does not improve the model. If you guessed the To account for the number of parameters this would also get you some points, But more precisely we are talking about the degrees of freedom.

$R_{a d j}^{2} = 1 - \frac{(1 - R^{2}) (n - 1)}{n - k - 1}$

where $n$ represents the number of data points in our dataset, $k$ the number of independent variables, and $R^{2}$ represents the R-squared values determined by the model (-1 i.e. interecept is not a parameter). So the answer is?

Answer to Question 11.20:

To account for the number of degrees of freedom!

Exercise 11.21 What is the correct definition of the variance inflation factor?

This is theory, you just have to remember it!

Answer to Question 11.21:

$\frac{1}{1 - R^{2}}$

Exercise 11.22 What are the consequences of collinearity among regressors?

As you may know Multicollinearity is problem that you can run into when you’re fitting a regression model, or other linear model. It refers to predictors that are correlated with other predictors in the model. Unfortunately, the effects of multicollinearity can feel murky and intangible, which makes it unclear whether it’s important to fix. Multicollinearity results in unstable parameter estimates which makes it very difficult to assess the effect of independent variables on dependent variables.

Let’s see that from another pov:

Consider the simplest case where $Y$ is regressed against $X$ and $Z$ such that $Y = α + β_{1} X + β_{2} Z + ϵ$ and where $Z$ and $Z$ are highly positively correlated. Then the effect of $X$ on $Y$ is hard to distinguish from the effect of $Z$ on $Y$ because any increase in $X$ tends to be associated with an increase in $Z$ . Now let’s also consider th pathological case where $X = Z$ highlights this further. $Y = α + β_{1} X + β_{2} Z + ϵ$ -> $Y = α + (β_{1} + β_{2}) X + 0 Z + ϵ$ then both of the two variables would be indistinguishable.

Answer to Question 11.22:

Estimators become unstable

Exercise 11.23 Using the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

Which variables are retained in the model? (retained means tratteresti)

This has cause many troubles too. The idea here is to fit many linear regression (multiple ones) and iteratively check collinearity and significance having buried in mind that We should retain in a model only statistically significant predictors which are not collinear. load carData and car, you are expected run vif (the only way we know we can test multicollinearity).

then:

Answer to Question 11.23:

first attempt:

library(carData)
library(car)
data("Wong")
wong_regression = lm(piq ~ age + days + duration, data = Wong)
summary(wong_regression)

From here you see that age and days are not significant, indeed duration is. However days havign .13 as p values is much more significant than age which accounts for .38 Let’s also check collinearity for this uncorrectly specified model. They all look good since their values are all <10.

Then we mnay want to see how the model, behaves by cancelling out age and keeping days, so:

wong_regression_2 = lm(piq ~ days + duration, data = Wong)

In this iteration we verify that duration becomes even more important since now has ***. However days just got worst. We finally remove it too. We don’t check vif() we have already done that and we do not expect that a subset of non collinear varibales (as before) now become collinear. As a result:ù

wong_regression_3 = lm(piq ~ duration, data = Wong)

In the end we only retain duration

Exercise 11.24 sing the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

What is the value of the adjusted R squared in the best model

We already stated which is the best model, now we look for the R-squared in the summary!

Answer to Question 11.24:

summary(wong_regression_3)

resulting in 0.02618

Exercise 11.25 sing the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

What is the estimated coefficient of the variable duration in the best model?

We already stated which is the best model, now we look for the R-squared in the summary!

Answer to Question 11.25:

wong_regression_3$coefficients[2]

resulting in -0.09918208

you can also directly look it through the summary

summary(wong_regression_3)

Exercise 11.26 sing the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

What is the estimated value of the intercept in the best model?

Answer to Question 11.26:

wong_regression_3$coefficients[1]

resulting in 88.97380549

you can also directly look it through the summary

summary(wong_regression_3)

Exercise 11.27 sing the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

What is the p-value of the variable duration in the best model?

Now look for the p-value of duration

Answer to Question 11.27:

summary(wong_regression_3)

resulting in duration p-value: 0.00183

Exercise 11.28 sing the dataset Wong from the R library carData, estimate a multiple linear regression where the variable piq is expressed as a function of age, days and duration.

After the check of collinearity and of significance choose the best model.

What is the value of the R square in the best model

Now for the R square

Answer to Question 11.28:

summary(wong_regression_3)

result : 0.02913

Exercise 11.29 Using the dataset iris, test if the average of the variable Sepal.Length changes significantly in the three Species considered. Report here the p-value of the appropiate test.

We look at Species (we have already gone through that during lecture) by inspecting the dataset. What we see is that Species has three categories setosa, versicolor and virginica. If we would like to compare means across these 3 different categories we can’t use t.test() since they are 3. Instead we use ANOVA with the aov(). Sintax is similar to linear models. We saw this when we were trying to tackle “long” format data vs. “wide” format data.

Answer to Question 11.29:

test_species = aov(Sepal.Length~Species, data = iris)
summary(test_species)

resulting in 0.0000000000000002, very significant. We can conclude that: The ANOVA (formula: Sepal.Length ~ Species) suggests that the main effect of Species is statistically significant and large.

Exercise 11.30 Using the dataset iris, test if the average of the variable Sepal.Length differs significantly in the three Species, Report here the value of the test statistic.

We take the exact same test as before and we look for the statistic

Answer to Question 11.30:

summary(test_species)

Here you look for the F statistics: F = 119.3

10 💻 Intermediate sample Q

12 💻 How dummy vars work